Quick Start
Project
A Project contains (multiple) simulation inputs, outputs and options.
Create or Open Project is the starting point for working with GibbsStudio. Saving the project, saves it to a binary “.hfst” file.
Graphical Interface Layout
The graphical interface contains the following parts:
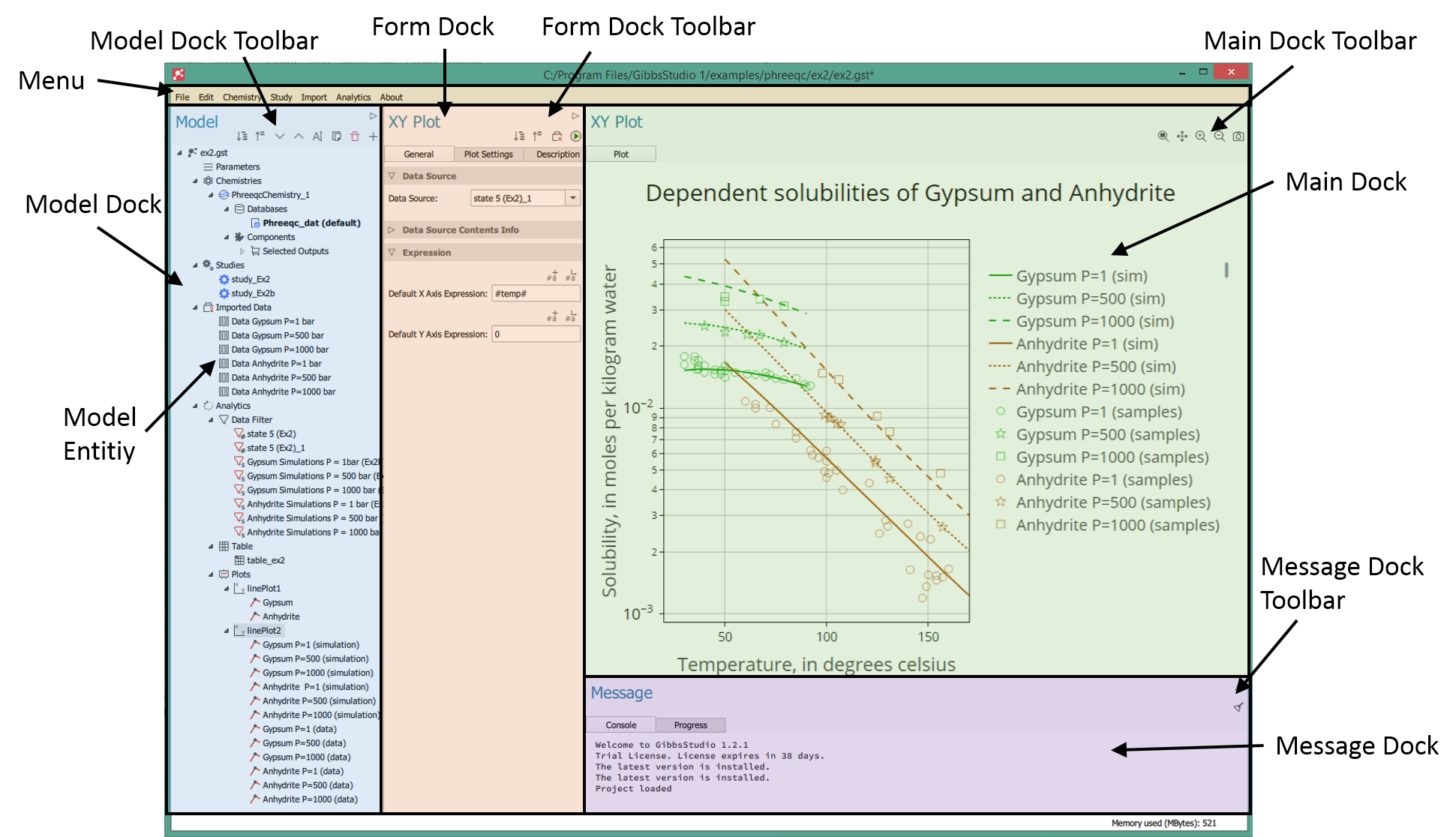
They provide the following functionalities:
Menu: Offers access to tools and actions.
Model Dock: Shows all the entities of the current project. Different actions such as create/remove/solve appear when right-clicking the selected entity
Form Dock: Shows information and options of the selected entity. The Form Dock Toolbar offers actions such as “Run”, “Update” or “Import”.
Main Dock: Shows detailed information, tables or plots for the selected entity.
Message Dock: Shows messages and study progress information to the user.
Running Existing Phreeqc Input
This section tries to explain to current Phreeqc users how to run their regular Phreeqc Files in GibbsStudio.
Create a New Project
The first step is to create a project to store all our inputs and outputs:
Click on “File->New Project” to create a new Project.
Click on “File->Save” and save it with the desired file name.
Set Up Phreeqc Lab
When creating a Project, a Phreeqc Lab entity is automatically added to the Models branch. The added Phreeqc Lab contains an Imported Database with the latest phreeqc.dat database version already loaded, a default Selected Output and a default Model with a simple Phreeqc Input.
Databases
The databases branch contains the different Phreeqc databases. The item bolded is the “default” one. The default item can be easily changed using the right click and clicking on “Set as default” on a different item. The default item will be the used by the studies and other elements if the user does not set it to an specific item.
If you rather load a different database, follow these steps:
In the Model Dock, right-click on Databases and add Imported Database.
In the Model Dock, right-click on the freshly created database and rename it to a name of your choice using Rename action.
With the new database selected, click in the Main Dock toolbar on the Load Text File In Editor button and select the database file you want to load. If you prefer, you can also paste the database text directly in the Main Dock editor.
Import Database by clicking in the Form Dock toolbar on the Import Database button. Once the database is loaded, its information is accessible from other entities such as Selected Output or Phreeqc Study

Selected Output
To make data available for later GibbsStudio postprocessing (tables, plots, etc.) a Selected Output is required:
In the Model Dock, right-click on Selected Outputs and add Selected Output.
In the Model Dock, select the freshly created selected output.
In the Form Dock, set the database combo box to the “Database” of your choice.
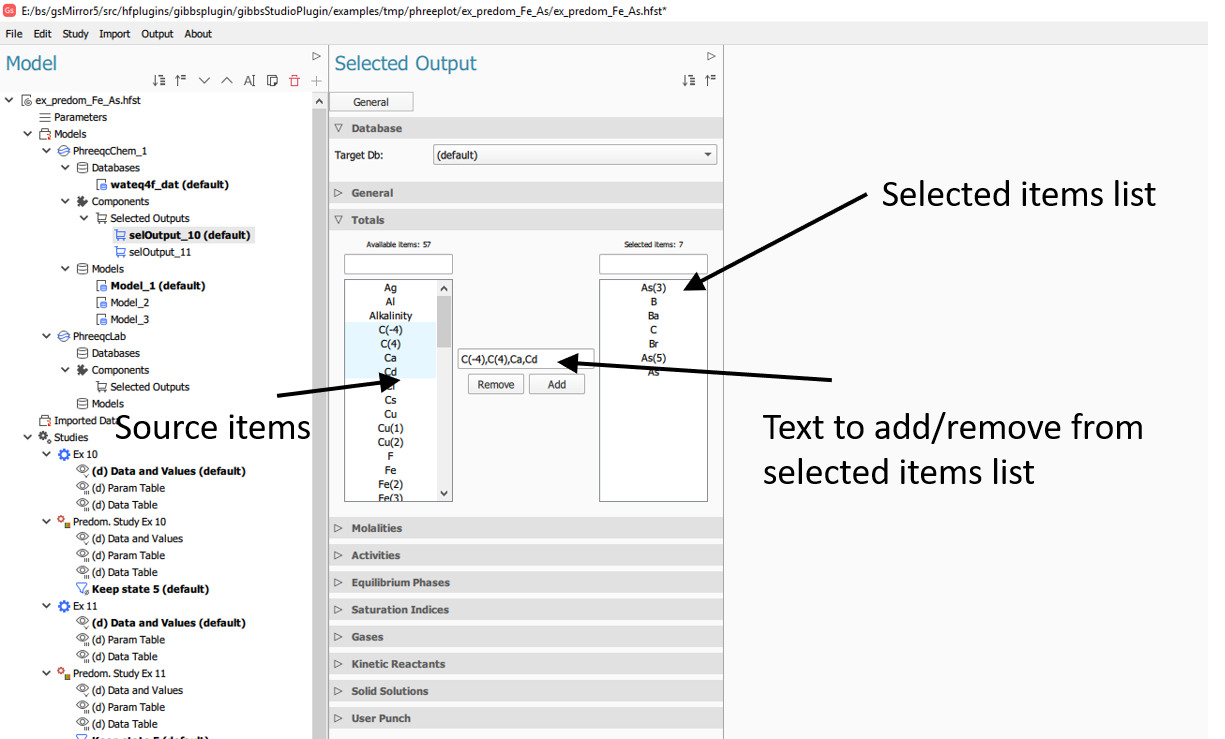
In the Form Dock, add the desired outputs, either by adding text to the selected items box list or by selecting, with the mouse, available items from the source list.
Model
Models are Phreeqc inputs.
They can be loaded in the same way than databases. Note that certain Phreeqc Keywords related with output settings (USER_PLOT, SELECTED_OUTPUT, DATABASE) are not compatible with the GibbsStudio workflow. During the import these words are removed. These changes should not affect the input but a user check is encoraged.
Set Up and run a Phreeqc Study
Phreeqc Study is the entity containing that joins the Phreeqc Input Model and the GibbsStudio simulation settings. To set it up:
In the Model Dock, right-click on Studies and Add Phreeqc Study.
In the Phreeqc Study Form Dock, with the created study in the Model Dock selected, pick the target Phreeqc Lab and the Model (also the Database and Selected Output if they are not set in the Model) created in the previous steps,
Run Study. Click on Solve button in the Form Dock Toolbar.
In the Main Dock, check the generated Phreeqc output files in the “Results” tab and the Selected Output in the “Data” tab.

Data Views
The study contain different data tables with simulation results (as a SQL database). Under the “Study” branch some default “Views” are created after solving the study.
The views are the one in charge to manage these data tables (join data tables, filter dome values) according the user needs. Some specific views are available (Table View, Filter by String View, …). Note that the user can also create its own SQL specific query.
Some specific for views Phreeqc are available which offer filter data for the following selected_output fields: “param”, “sim”, “state_id”, “step”, “soln”. For each filter the indices to filter can be selected.
To filter phreeqc study data:
In Model Dock, right-click on the Phreeqc Study and add the desired view filter.
Select source view.
Select the desired indices.
Click on Compute in the Form Dock Toolbar to see the filtered results.
Create a Plot
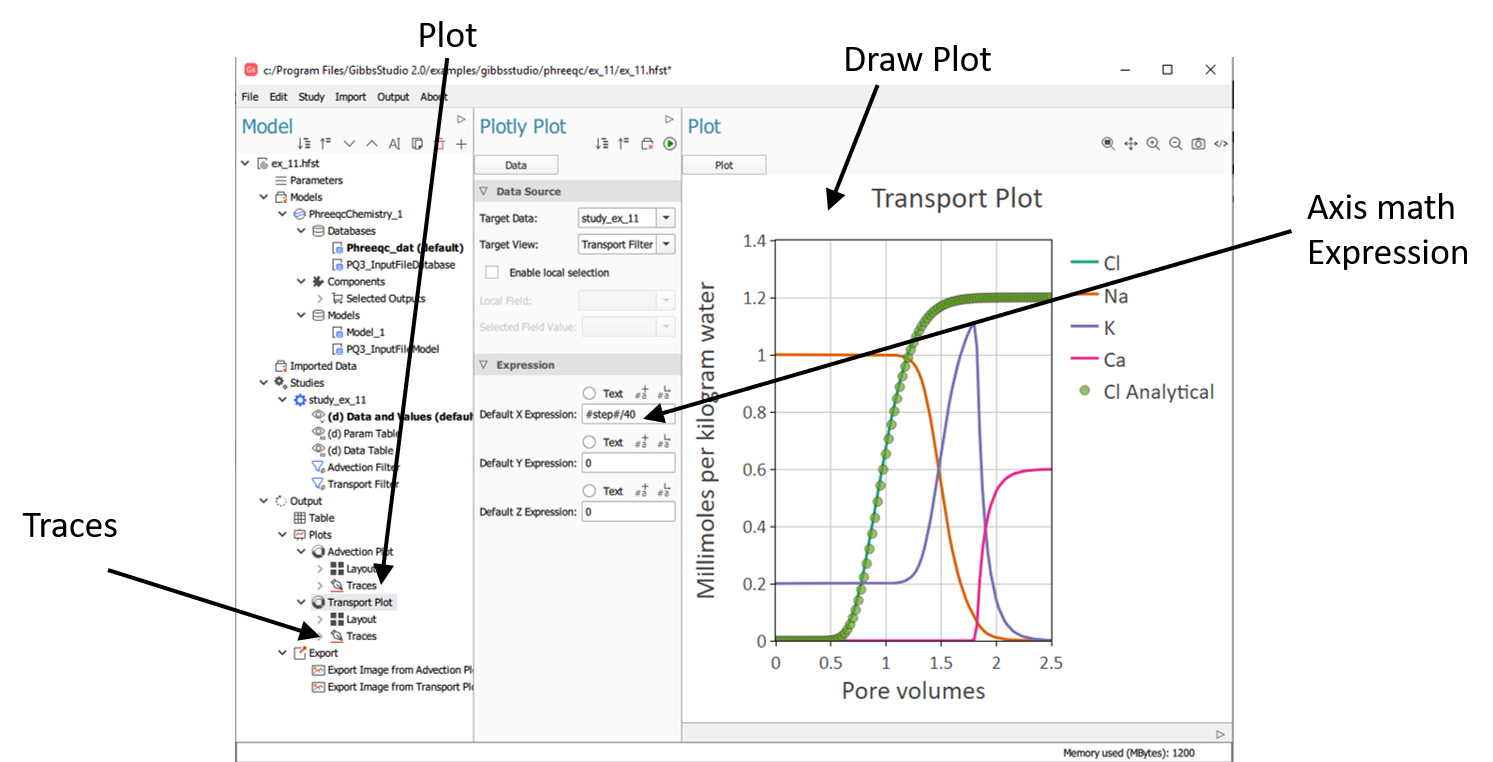
In the Model Dock, right-click on Plots and add a 2D ord 3D Plot.
In the created Plot, set the Data Source Target Data and Target View to the Study and to View that contains the data you want to plot.
Create a Trace.
In the created “Trace”, set “Data Source” to the “Study” or “Filter”. “(Parent)” value means that the series points to the same data as the plot (parent in the tree hierarchy). This is the default value.
Set a math expression for “X Axis” and “Y Axis”. Variables can be added using the buttons above the expression.
Adjust the plot and series settings in the Form dock settings tab.
Parameterize a Phreeqc Input
A Phreeqc Study can be parameterized:
Create a new Parameter in Model Dock Parameters entity by adding it to the Form Dock Parameter Definition Table.
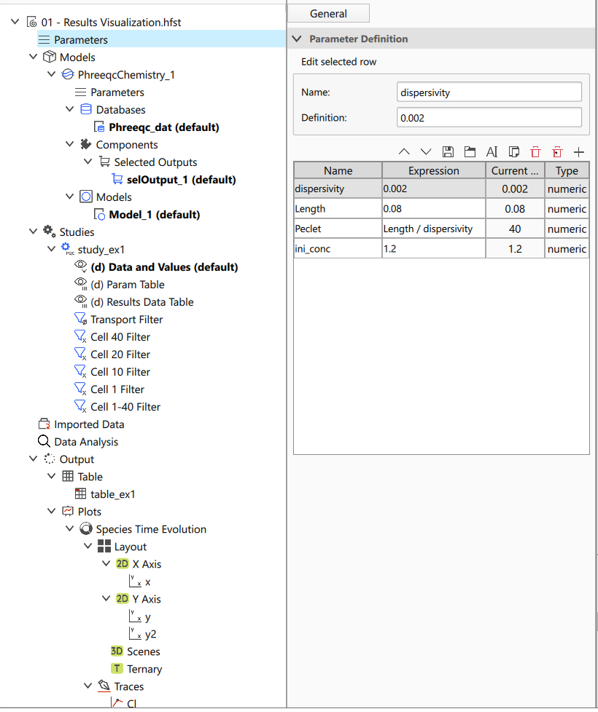
Use the parameter expression enclosed by @{}@ in “Phreeqc Study” input text editor, e.g. @{my_param}@ or @{$my_param+1$}@ if you want to perform a mathematical operation.

Math Expressions in Results
All kind of math expressions can be used in several parts of the program.
The use of variables
Variables should be enclosed by hash symbols (e.g. #someVariable#). This is to prevent issues with variables that contain mathematical symbols in their name.
The use of operators and functions
Arithmetic & Assignment Operators
OPERATOR |
DEFINITION |
|---|---|
“+” |
Addition between x and y. (eg: x + y) |
“-” |
Subtraction between x and y. (eg: x - y) |
“*” |
Multiplication between x and y. (eg: x * y) |
“/” |
Division between x and y. (eg: x / y) |
“%” |
Modulus of x with respect to y. (eg: x % y) |
“^” |
x to the power of y. (eg: x ^ y) |
Equalities & Inequalities
OPERATOR |
DEFINITION |
|---|---|
== or = |
True only if x is strictly equal to y. (eg: x == y) |
<> or != |
True only if x does not equal y. (eg: x <> y or x != y) |
< |
True only if x is less than y. (eg: x < y) |
<= |
True only if x is less than or equal to y. (eg: x <= y) |
> |
True only if x is greater than y. (eg: x > y) |
>= |
True only if x greater than or equal to y. (eg: x >= y) |
Boolean Operations
OPERATOR |
DEFINITION |
|---|---|
true |
True state or any value other than zero (typically 1). |
false |
False state, value of exactly zero. |
and |
Logical AND, True only if x and y are both true. (eg: x and y) |
mand |
Multi-input logical AND, True only if all inputs are true. Left to right short-circuiting of expressions. (eg: mand(x > y, z < w, u or v, w and x)) |
mor |
Multi-input logical OR, True if at least one of the inputs are true. Left to right short-circuiting of expressions. (eg: mor(x > y, z < w, u or v, w and x)) |
nand |
Logical NAND, True only if either x or y is false. (eg: x nand y) |
nor |
Logical NOR, True only if the result of x or y is false (eg: x nor y) |
not |
Logical NOT, Negate the logical sense of the input. (eg: not(x and y) == x nand y) |
or |
Logical OR, True if either x or y is true. (eg: x or y) |
xor |
Logical XOR, True only if the logical states of x and y differ. (eg: x xor y) |
xnor |
Logical XNOR, True iff the biconditional of x and y is satisfied. (eg: x xnor y) |
& |
Similar to AND but with left to right expression short circuiting optimisation. (eg: (x & y) == (y and x)) |
Similar to OR but with left to right expression short circuiting optimisation. (eg: (x | y) == (y or x)) |
General Purpose Functions
FUNCTION |
DEFINITION |
|---|---|
abs |
Absolute value of x. (eg: abs(x)) |
avg |
Average of all the inputs. (eg: avg(x,y,z,w,u,v) == (x + y + z + w + u + v) / 6) |
ceil |
Smallest integer that is greater than or equal to x. |
clamp |
Clamp x in range between r0 and r1, where r0 < r1. (eg: clamp(r0,x,r1)) |
equal |
Equality test between x and y using normalised epsilon |
erf |
Error function of x. (eg: erf(x)) |
erfc |
Complimentary error function of x. (eg: erfc(x)) |
exp |
e to the power of x. (eg: exp(x)) |
expm1 |
e to the power of x minus 1, where x is very small. (eg: expm1(x)) |
floor |
Largest integer that is less than or equal to x. (eg: floor(x)) |
frac |
Fractional portion of x. (eg: frac(x)) |
hypot |
Hypotenuse of x and y (eg: hypot(x,y)=sqrt(x*x + y*y)) |
iclamp |
Inverse-clamp x outside of the range r0 and r1. Where r0 < r1. If x is within the range it will snap to the closest bound. (eg: iclamp(r0,x,r1) |
inrange |
In-range returns ‘true’ when x is within the range r0 and r1. Where r0 < r1. (eg: inrange(r0,x,r1) |
log |
Natural logarithm of x. (eg: log(x)) |
log10 |
Base 10 logarithm of x. (eg: log10(x)) |
log1p |
Natural logarithm of 1 + x, where x is very small. (eg: log1p(x)) |
log2 |
Base 2 logarithm of x. (eg: log2(x)) |
logn |
Base N logarithm of x. where n is a positive integer. (eg: logn(x,8)) |
max |
Largest value of all the inputs. (eg: max(x,y,z,w,u,v)) |
min |
Smallest value of all the inputs. (eg: min(x,y,z,w,u)) |
mul |
Product of all the inputs. (eg: mul(x,y,z,w,u,v,t) == (x * y * z * w * u * v * t)) |
ncdf |
Normal cumulative distribution function. (eg: ncdf(x)) |
nequal |
Not-equal test between x and y using normalised epsilon |
pow |
x to the power of y. (eg: pow(x,y) == x ^ y) |
root |
Nth-Root of x. where n is a positive integer. (eg: root(x,3) == x^(1/3)) |
round |
Round x to the nearest integer. (eg: round(x)) |
roundn |
Round x to n decimal places (eg: roundn(x,3)) where n > 0 and is an integer. (eg: roundn(1.2345678,4) == 1.2346) |
sgn |
Sign of x, -1 where x < 0, +1 where x > 0, else zero. (eg: sgn(x)) |
sqrt |
Square root of x, where x >= 0. (eg: sqrt(x)) |
sum |
Sum of all the inputs. (eg: sum(x,y,z,w,u,v,t) == (x + y + z + w + u + v + t)) |
swap <=> |
Swap the values of the variables x and y and return the current value of y. (eg: swap(x,y) or x <=> y) |
trunc |
Integer portion of x. (eg: trunc(x)) |
Trigonometry Functions
FUNCTION |
DEFINITION |
|---|---|
acos |
Arc cosine of x expressed in radians. Interval [-1,+1] (eg: acos(x)) |
acosh |
Inverse hyperbolic cosine of x expressed in radians. (eg: acosh(x)) |
asin |
Arc sine of x expressed in radians. Interval [-1,+1] (eg: asin(x)) |
asinh |
Inverse hyperbolic sine of x expressed in radians. (eg: asinh(x)) |
atan |
Arc tangent of x expressed in radians. Interval [-1,+1] (eg: atan(x)) |
atan2 |
Arc tangent of (x / y) expressed in radians. [-pi,+pi] eg: atan2(x,y) |
atanh |
Inverse hyperbolic tangent of x expressed in radians. (eg: atanh(x)) |
cos |
Cosine of x. (eg: cos(x)) |
cosh |
Hyperbolic cosine of x. (eg: cosh(x)) |
cot |
Cotangent of x. (eg: cot(x)) |
csc |
Cosecant of x. (eg: csc(x)) |
sec |
Secant of x. (eg: sec(x)) |
sin |
Sine of x. (eg: sin(x)) |
sinc |
Sine cardinal of x. (eg: sinc(x)) |
sinh |
Hyperbolic sine of x. (eg: sinh(x)) |
tan |
Tangent of x. (eg: tan(x)) |
tanh |
Hyperbolic tangent of x. (eg: tanh(x)) |
deg2rad |
Convert x from degrees to radians. (eg: deg2rad(x)) |
deg2grad |
Convert x from degrees to gradians. (eg: deg2grad(x)) |
rad2deg |
Convert x from radians to degrees. (eg: rad2deg(x)) |
grad2deg |
Convert x from gradians to degrees. (eg: grad2deg(x)) |
Control Structures
STRUCTURE |
DEFINITION |
|---|---|
if |
If x is true then return y else return z. eg: 1. if (x, y, z) 2. if ((x + 1) > 2y, z + 1, w / v) 3. if (x > y) z; 4. if (x <= 2*y) { z + w }; |
if-else |
The if-else/else-if statement. Subject to the condition branch the statement will return either the value of the consequent or the alternative branch. eg: 1. if (x > y) z; else w; 2. if (x > y) z; else if (w != u) v; 3. if (x < y) { z; w + 1; } else u; 4. if ((x != y) and (z > w))
|
switch |
The first true case condition that is encountered will determine the result of the switch. If none of the case conditions hold true, the default action is assumed as the final return value. This is sometimes also known as a multi-way branch mechanism. eg: switch {
} |